集中趋势的定义
集中趋势:平均或有代表性的数值被称为集中趋势。目的是确定一个代表分布中心的值来描述一组数据的分布。理想上,这个中心值是在分布中能够最好代表所有个体的值。
确定集中趋势没有统一的、标准化的方法,没有一种测量集中趋势的代表性数值的方法适用于所有的情况。
平均数
总体平均数用 μ 代表,样本平均数由 M 或 Χ 代表。
平均数:数据的总和除以数据的个数
μ = ∑X/N(总数的个数)
M = ∑X/n(样本的个数)
中数
中数:中数是恰好将一个分布一分为二的数值,分布中恰好50%的个体具有小于或等于中数的数值,另一半恰好大于或等于中数。目的是确定一个分布的精确中点。
众数
众数:在一组分数中,最常出现的值。
在一个频数分布图中,具有2个众数的分布被称为双峰分布,具有多于2个众数的分布被称为多峰分布。有时候,具有数个等高点的分布也被称为无众数。
通常,双峰分布说明在同一个总体(样本)中存在两个不同的、有区别的个体组。
众数也经常被用来指那些具有相对高频数的值。较高的刘高峰被称为主要众数,较矮的高峰被称为次要众数。
选择集中趋势测量的原则
集中趋势的目的是找出能够最好代表整个分布的值。
平均数通常是最好的一种。
使用中数的情况:
- 有极端数值和偏态分布
- 有未确定数值
- 尾端开放式分布(分布的类别没有上下限时)
- 顺序量表
使用众数的情况:
- 称名量表
- 离散变量
- 描述形状(表示了高峰的位置)
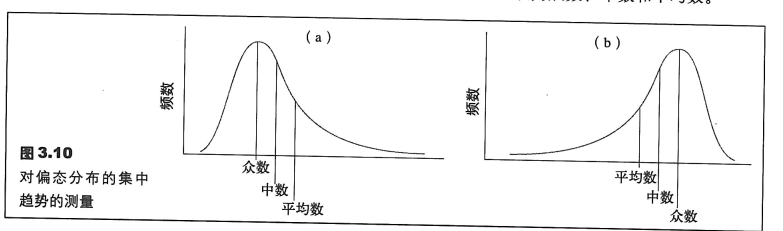
集中趋势和分布形状
对称分布
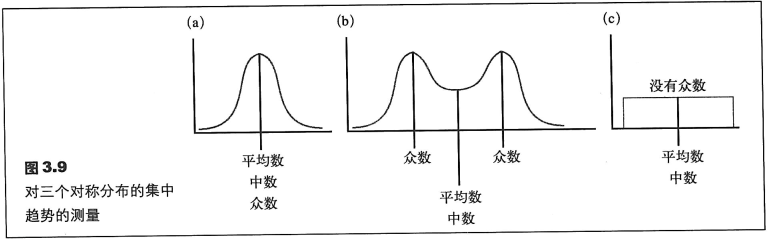
偏态分布